Shifted Gompertz distribution

Shifted Gompertz distribution is useful distribution which can be used to describe time needed for adopting new innovation within the market. Recent studies showed that it outperforms Bass model of diffusion in some cases¹.

Its pdf is given by

Below we show what happens if we increase parameter (inverse of propensity to adopt) for different values of appeal of innovation. Higher parameter is set more density mode is shifted away from .

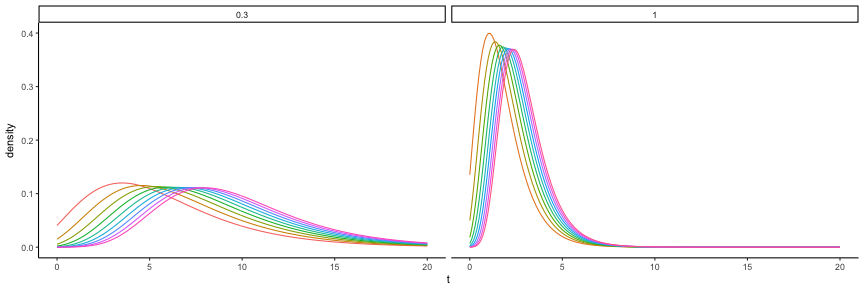
This distribution do not have closed form solutions for moments. If we want to calculate them and also simulate data for model validation we need to be able to sample from it. Luckily there is a simple way of producing samples from arbitrary density:

Fundamental Theorem of Simulation.
Simulating

is equivalent to simulating

Direct corollary introduces convenient way of simulating from target distribution:

Accept-Reject algorithm.
Let and let be a density function that satisfies for some constant and . Then, to simulate it is sufficient to generate pair

until

Function is sometimes called envelope function. More tight the inequality the more efficient sampling will be.

Simulating from Shifted Gumbel distribution

Let’s assume for a moment that our density has bounded support. Below we plot an example of using Accept-Reject method for sampling from target density with simple constant envelope function:

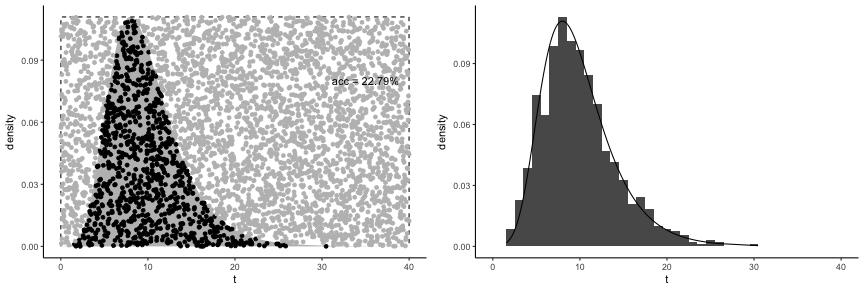
This way of simulating distribution works but is not particularly efficient as more than 75% of sample is rejected and that’s with assumption that the support of target density is in . If we would extend support of the target density to further away from we would see increasing drop of sampler efficiency.

We can easily improve our sampling method by noticing the following inequality:

This will provide us nice majorization function for the tail of shifted Gompertz distribution by scaled exponential density.

In order to make it more tight around mode of our target density we can define improved envelope function as:

where is a point where envelope function reaches maximum of shifted Gompertz density and is a value of the density at this point.

Of course is not a density itself. Since it is integrable we can recover density as

which is mixture of uniform and truncated exponential distribution.

Algorithm pseudocode

select component with probabilities p1(b, eta) and p2(b, eta)
Repeat
  sample y from selected density component
  sample u from U[0, h'(y|b, eta)]
Until u < p(y|b, eta)

Sampling results

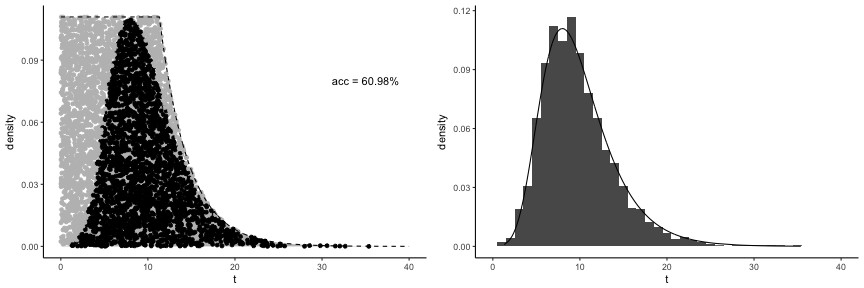
Kolmogorov Smirnov test

It’s straightforward to test whether we sample from correct distributions by comparing empirical cumulative distribution function with exact one.

	One-sample Kolmogorov-Smirnov test

data:  s
D = 0.0018236, p-value = 0.8936
alternative hypothesis: two-sided

Perfect! Sampled data distribution is indistinguishable from theoretical density. We can also inspect sampling results visually:

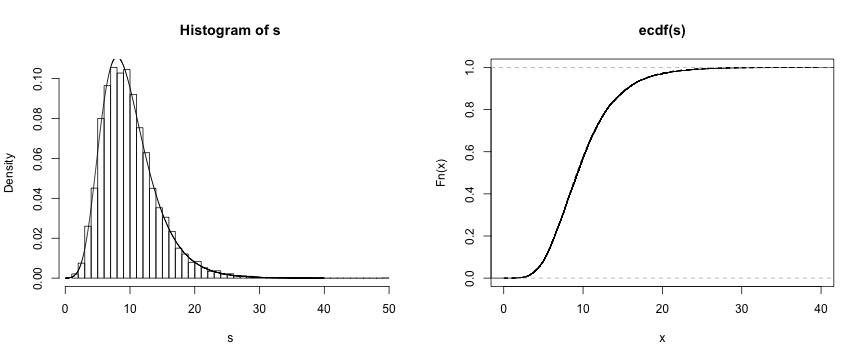
Summary

We created from scratch new sampler for shifted Gompertz distribution :) and it’s fairly efficient: for one milion of sampled values it takes latter algorithm only 0.138 of a second.

Code for this post can be found here: https://github.com/jakubglinka/posts/tree/master/diffusion_part1